The Classification of Permutation Groups with Maximum Orbits
DOI:
https://doi.org/10.24297/jam.v15i0.7926Keywords:
permutation group, bounded movement, orbits, permutation group, bounded movement, orbitsAbstract
Let G be a permutation group on a set with no fixed points in and let m be a positive integer. If no element of G moves any subset of by more than m points (that is, if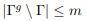 
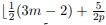
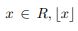
for every and g 2 G), and the lengths two of orbits is p, and the restof orbits have lengths equal to 3. Then the number t of G-orbits in is at most 
Moreover, we classifiy all groups for
is hold.(For 
denotes the greatest integer less than or equal to x.)
Downloads
References
L. Brailovsky, Structure of quasi-invariant sets, Arch. Math.,59 (1992),322- 326.
L. Brailovsky, D. Pasechnix , C. E. Praeger, Subsets close to invarianr subset of quasi-invariant subsets for group actions ,,Proc. Amer. Math.Soc. ,123(1995),2283-2295.
C. E. Praeger,On permutation groups with bounded movement,J.Algebra ,144(1991),436-442.
C. E. Praeger, The separation theorem for group actions, in ”ordered Groups and Infinite Groups”(W. charles Holland, Ed.), Kluwer Academic, Dordrecht/ Boston/ Lond, 1995.
A. Hassani, M. Khayaty, E. I. Khukhro and C. E. Praeger, Transitive permutation groups with bounded movement having maximum degree. J. Algebra,214(1999),317-337.
J. R. Cho, P.S.Kim, and C. E. Praeger, The maximal number of orbits of a permutation Group with Bounded Movement, J.Algebra,214 (1999),625- 630.
P. M. Neumann, The structure of finitary Permutation groups, Arch. Math. (Basel) 27(1976),3-17.
B. H. Neumann, Groups covered by permutable subsets, J. London Math soc., 29(1954), 236-248.
P. M. Neumann, C. E. Praeger, On the Movement of permutation Group, J. Algebra, 214, (1999)631-635.
Downloads
Published
How to Cite
Issue
Section
License
All articles published in Journal of Advances in Linguistics are licensed under a Creative Commons Attribution 4.0 International License.
