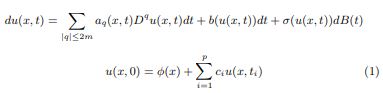A Unique Solution of Stochastic Partial Differential Equations with Non-Local Initial condition
DOI:
https://doi.org/10.24297/jam.v16i0.8018Keywords:
Stochastic partial differential equation, Pathwise uniqueness, Bihari’s inequality.Abstract
In this paper, we shall discuss the uniqueness ”pathwise uniqueness” of the solutions of stochastic partial differential equations (SPDEs) with non-local initial condition,
We shall use the Yamada-Watanabe condition for ”pathwise uniqueness” of the solutions of the stochastic differential equation; this condition is weaker than the usual Lipschitz condition. The proof is based on Bihari’s
inequality.
Downloads
Download data is not yet available.
Downloads
Published
2019-01-31
How to Cite
El-Borai, M. M. M., & S.A., A. T. (2019). A Unique Solution of Stochastic Partial Differential Equations with Non-Local Initial condition. JOURNAL OF ADVANCES IN MATHEMATICS, 16, 8226–8233. https://doi.org/10.24297/jam.v16i0.8018
Issue
Section
Articles
License
All articles published in Journal of Advances in Linguistics are licensed under a Creative Commons Attribution 4.0 International License.
