Least Squares Estimator for Vasicek Model Driven by Fractional Levy Processes

qingbo wang; Xiuwei Yin

doi:10.24297/jam.v14i2.7839

Authors

qingbo wang Anhui Normal University
Xiuwei Yin Anhui Normal University

DOI:

https://doi.org/10.24297/jam.v14i2.7839

Keywords:

least squares estimator, Stochastic differential equations, fraction Levy processes, asymptotic distribution.

Abstract

In this paper, we consider parameter estimation problem for Vasicek model driven by fractional lévy processes defined

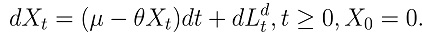
We construct least squares estimator for drift parameters based on time?continuous observations, the consistency and asymptotic distribution of these estimators are studied in the non?ergodic case. In contrast to the fractional Vasicek model, it can be regarded as a Lévy generalization of fractional Vasicek model.

Downloads

Download data is not yet available.

Author Biography

Xiuwei Yin, Anhui Normal University

School of mathematics and statistic, Anhui Normal University, Wuhu 241000, P.R. China

References

C. Bender, A. Lindner, M. Schicks. Finite variation of fractional Lévy processes. J. Theor. Probab. 25 (2012) 594?612

J. P. Bishwal. Parameter estimation in stochastic differential equations. Berlin: Springer. 24 (2008).

F. Comte, E. Renault. Long memory in continuous?time stochastic volatility models. J. Econometr. 8 (1998) 291?323.

F. Comte, L. Coutin and E. Renault, Affine fractional stochastic volatility models. Ann Finance 8(23) (2012) 337?378.

S. Corlay, J. Lebovits and J. L. Véhel, Multifractional stochastic volatility models. J. Econometr. 24(2) (2014) 364?402.

H. M. Dietz, Y. A. Kutoyants. Parameter estimation for some non?recurrent solutions of SDE. Statist. Decisions. 21 (2003) 29?46.

H. Fink, C. Klüppelberg. Fractional Lévy?driven Ornstein?Uhlenbeck processes and stochastic differential equations. Bernoulli. 17 (2011) 484?506.

Y. Hu, D. Nualart. Parameter estimation for fractional Ornstein?Uhlenbeck process. Statist. Probab. Lett. 80 (2010) 1030?1038.

Y. A. Kutoyants. Statistical Inference for Ergodic Diffusion Processes. Berlin, Heidelberg: Springer, 2004.

T. Marquardt. Fractional Lévy processes with an application to long memory moving average processes. Bernoulli 12(6) (2006) 1099?1126.

B. L. S. Prakasa Rao. Parametric estimation for linear stochastic delay differential equations driven by fractional Brownian motion. Random Oper. Stochastic Equations. 16 (2008) 27–38.

G. Samorodnitsky and M. Taqqu. Stable Non?Gaussian Random processes: Stochastic Models with Infinite Varice. Champman & Hall, New York. 1994.

K. Sato. Lévy Processes and Infinitely Divisible Distributions . Cambridge: Cambridge University Press, 1999.

H. Tikanmäki, Y. Mishura. Fractional Lévy processes as a result of compact interval integral transformation. Stoch. Anal. Appl. 29 (2011) 1081?1101.

O. Vasicek. An equilibrium characterization of the term structure. J. Financial Ecori. 5(2)(1977) 177?188.

W. Xiao, J. Yu. Asymptotic theory for estimating the persistent parameter in the fractional vasicek model. Singapore Management University, School of Economics, Paper No. 9?2016.