Stability of Cubic Functional Equation in Random Normed Space

Sandra Pinelas; V. Govindan; K. Tamilvanan

doi:10.24297/jam.v14i2.7614

Authors

Sandra Pinelas Academia Militar, Portugal
V. Govindan Sri Vidya Mandir Arts & Science College, India
K. Tamilvanan Sri Vidya Mandir Arts & Science College, India

DOI:

https://doi.org/10.24297/jam.v14i2.7614

Keywords:

Cubic Functional Equation, Fixed Point, Hyers-Ulam stability, Random Normed Space

Abstract

In this paper, we present the Hyers-Ulam stability of Cubic functional equation.

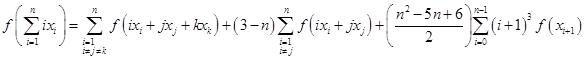
where n is greater than or equal to 4, in Random Normed Space.

Downloads

Download data is not yet available.

Author Biographies

Sandra Pinelas, Academia Militar, Portugal

Departmento de Ciencias Exatas e Engenharia, Academia Militar, Portugal

V. Govindan, Sri Vidya Mandir Arts & Science College, India

Sri Vidya Mandir Arts & Science College, Katteri, Uthangarai, Tamilnadu, India

K. Tamilvanan, Sri Vidya Mandir Arts & Science College, India

Sri Vidya Mandir Arts & Science College, Katteri, Uthangarai, Tamilnadu, India

References

J. Aczel and J. Dhombres, Functional Equations in Several Variables, Cambridge University Press, 1989.

E. Baktash, Y. J. Cho, M. Jalili, R. Saadati and S. M. Vaezpour, On the Stability of Cubic Mappings and Quadratic Mappings in Random Normed Spaces, J. Ineq. Appl. Article ID: 902187, (2008).

Y. J. Cho, T. M. Rassias, R. Saadati, stability of Functional Equations in Random Normed Spaces, springer, New York, (2013).

M. Eshanghi Gordji, J. M. Rassias and M. Bavand Savadkouhi, Approximation of the Quadratic and Cubic Functional Equation in RN-Spaces, European J. pure. Appl. Math., Vol. 2(4), (2009), 494-507.

K. W. Jun and H. M. Kim, The Generalized Hyers-Ulam-Rassias Stability of a Cubic Functional Equation, J. Math. Analysis and Appl., Vol. 274(2), (2002), 867-878.

H. A. Kenary, H. Rezaei, S. Talebzadeh, S. J. Lee, stabilities of Cubic Mappings in Various Normed Spaces: Direct and Fixed Point Methods, J. Appl. Math.,Article ID: 546819, (2012).

D. Mihet and V. Radu, On the Stability of the Additive Cauchy Functional Equation in Random Normed Spaces, J. Math. Analysis and Appl., Vol. 343(1), (2008), 567-572.

D. Mihet, R. Saadati, S. M. Vaezpour, The Stability of the Quartic Functional Equation in Random Normed Space, Acta. Appl. Math., Vol. 110, (2010), 799-803.

S. Murthy, M. Arunkumar and V. Govindan, General Solution and Generalized Hyers-Ulam Stability of n-Dimensional Cubic Functional Equation in Various Space: Direct and Fixed-Point Methods, Int. J. Math. Appl., Vol. 4(1-D), (2016), 81-109.

S. Murthy, M. Arunkumar and V. Govindan and T. Namachivayam, General Solution and Four Types of Ulam – Hyers Stability Of -Dimensional Additive Functional Equation in Banach And Fuzzy Banach Spaces: Hyers Direct and Fixed-Point Methods, Int. J. Appl. Eng. Research, Vol. 11(1), (2016), 324-338.

S. Murthy, V. Govindhan and M. Sree Shanmuga Velan, Solution and Stability of Two Types Of N-Dimensional Quartic Functional Equation in Generalized 2-Normed Spaces, International Journal of Pure and Applied Mathematics, Vol. 111(2), (2016), 249-272.

K. Ravi, J.M. Rassias, Sandra Pinelas and R. Jamuna, A Fixed-Point Approach to the Stabilityof a Quadratic Quartic Functional Equation in Paranormed Spaces, PanAmerican Mathematical Journal, Vol. 24(2), (2014), 61–84.

Renu Chugh, Ashish, On the Stability of Functional Equations in Random Normed Spaces, Int. J. Computer Appl., Vol. 45(11), (2012).

Roji Lather, Kusum Dhingra, Stability of Quartic Functional Equation in Random 2-Normed Spaces, Int. J. Computer Appl., Vol. 147(2), (2016), 39-42.

R. Saadati, S. M. Vaezpour and Y. J. cho, A Note to Paper “On the Stability of Cubic Mappings and Quartic Mappings in Random Normed Spaces”, J. Ineq. Appl., DOI: 10.1155/2009/214530, (2009).

Sandra Pinelas, V. Govindan and K. Tamilvanan, Stability of Non-Additive Functional Equation, IOSR Journal of Mathematics, 14(2), (2018), 70-78.

Seong Sik Kim, John Michael Rassias, Nawab Hussain, Yeol Je Cho, Generalized Hyers-Ulam Stability of General Cubic Functional Equation in Random Normed Space, Filomat, Vol. 30(1), (2016), 89-98.

Shaymaa Alshybami, S. Mansour Vaezpour, Reza Saadati, Generalized Hyers-Ulam Stability of Mixed Type Additive-Quadratic Functional Equation in Random Normed Spaces, J. Math. Analysis, vol. 8(5), (2017), 12-26.

A. N. Sherstner, On the Notation of a Random Normed Space, Doklady Aka demii Nauk SSSr, Vol. 149, (1963), 280-283.

T. Z. Xu, J. M. Rassias, W. X. Xu, On Stability of a General Mixed Additive-Cubic Functional Equation in Random Normed Spaces, J. Inequl. Appl., Article ID: 328473, (2010).

S. Zhang, J. M. Rassias and R. Saadati, Stability of a Cubic Functional in Intuitionistic Random Normed Spaces, Appl. Math. Mech. Engl. Ed 31(1), (2010), 21-26.