Uniqueness for Entropy Solutions to fully Nonlinear Equations
DOI:
https://doi.org/10.24297/jam.v5i2.7239Keywords:
entropic solution, nonlinear elliptic equation, uniqueness solutionAbstract
Let X be a metric space,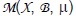 
the space of 
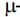measurable funtions, 
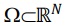be a domain whith boundary 
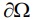and a(x; 
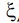) be an operator of Leray-Lions type. If 
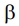and
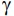are nondecreasing continuous function on R such that 
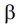(0) =
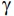(0) = 0 and (f; g) 
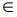L1 (X; 
;
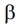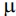), then, there exists a unique entropy solution u in M(X; B;
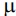) to the problem [a(.,Du)] + 
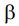(u) = and a(.,Du)v+
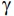(u) = g on
.
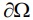Downloads
Download data is not yet available.
Downloads
Published
2013-12-23
How to Cite
KOURAICHI, C., & SIAI, A. (2013). Uniqueness for Entropy Solutions to fully Nonlinear Equations. JOURNAL OF ADVANCES IN MATHEMATICS, 5(2), 650–656. https://doi.org/10.24297/jam.v5i2.7239
Issue
Section
Articles
License
All articles published in Journal of Advances in Linguistics are licensed under a Creative Commons Attribution 4.0 International License.
