Characterizations of stability of first order linear Hahn difference equations

Abstract

Hahn introduced the difference operator Dq.wf(t) = f(qt + w) -f(t))/t(q -1+w) in 1949, where 0 < q < 1 and ! > 0 are fixed real numbers. This operator extends the classical difference operator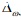  f(t) = (f(t +w)-f(t))/w as well as Jackson q- difference operator Dqf(t) = (f(qt) f(t))/(t(q- 1)). In this paper, our objective is to establish characterizations of many types of stability, like (uniform, uniform exponential, 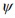-) stability of linear Hahn difference equations of the form D.w!x(t) = p(t)x(t) + f(t). At the end, we give two illustrative examples.