MEAN CURVATURE FLOW OF SUBMANIFOLDS WITH SMALL TRACELESS SECOND FUNDAMENTAL FORM

Abstract

Consider a family of smooth immersions F(; t) : M^_n 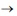 M^n+k of submanifolds in M^n+k moving by mean curvature flow 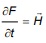= 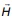, where  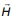is the mean curvature vector for the evolving submanifold. We prove that for any n >^_-2 and k>-1, the flow starting from a closed submanifold with small L²-norm of the traceless second fundamental form contracts to a round point in finite time, and the corresponding normalized flow converges exponentially in the C-topology, to an n-sphere in some subspace Mⁿ⁺¹ of M^n+k.