MODELLING NIGERIA POPULATION GROWTH RATE

Abstract

Thomas Robert Malthus Theory of population highlighted the potential dangers of over population. He stated that while the populations of the world wouldincrease in geometric proportions, the food resources available for them would increase in arithmetic proportions. This study was carried out to find the trend, fit a model and forecast for the population growth rate of Nigeria.The data were based on the population growth rate of Nigeria from 1982 to 2012 obtained from World Bank Data (data.worldbank.org). Both time and autocorrelation plots were used to assess the Stationarity of the data. Dickey-Fuller test was used to test for the unit root. Ljung box test was used to check for the fit of the fitted model. Time plot showed that the random fluctuations of the data are not constant over time. There was an initial decrease in the trend of the growth rate from 1983 to 1985 and an increase in 1986 which was constant till 1989 and then slight fluctuations from 1990 to 2004 and a general increase in trend from 2005 to 2012. There was a slow decay in the correlogram of the ACF and this implied that the process is non stationary. The series was stationary after second differencing, Dickey-Fuller = -4.7162, Lag order = 0, p-value = 0.01 at a= 0.05. The p-value (0.01) and concluded that there is no unit root i.e the series is stationary having d=2. Correlogram and partial correlogram for the second-order differenced data showed that the ACF at lag 1 and lag 5 exceed the significant bounds and the partial correlogram tailed off at lag 2.The identified order for the ARIMA(p,d,q) model was ARIMA(2,2,1). The estimate of AR1 co-efficient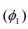 =1.5803 is observed to be statistically significant but the estimated value does not conforms strictly to the bounds of the stationary parameter hence was excluded from the model. 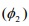=-0.9273 is observed to be statistically significant and conformed strictly to the bounds of the stationary parameter , hence 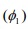was maintained in the model.

The estimate of MA1 co-efficient = - 0.1337 was observed to be statistically significant conformed strictly to the bounds of the parameter invertibility. For ARIMA (2, 2, 0) the estimate of AR1 co-efficient =1.5430 was observed to be statistically significant and not conformed strictly to the bounds of the parameter stationary, hence excluded from the model.

The estimate of AR 2 co-efficient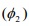=-0.9000 is observed to be statistically significant and conformed strictly to the bounds of the parameter stationary, hence retained in the model.

The ARIMA (2, 2, 0) is considered the best model. It has the smallest AIC. The Ljung test showed that residuals are random and  implies that the model is fit enough for the data. The forecast Arima function gives us a forecast of the Population Growth Rate in the next thirty eight (38) years, as well as 80% and 95% prediction intervals for those predictions i.e up to 2050.