FERMAT'S LAST THEOREM: ALGEBRAIC PROOF

Abstract

In 1995, A, Wiles announced, using cyclic groups, a proof of Fermat's Last Theorem, which is stated as follows: If is an odd prime and x; y; z are relatively prime positive integers, then .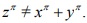  In this note, a proof of this theorem is offered, using elementary Algebra. It is proved that  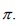if is an odd prime and x; y; z are positive inyegera satisfying 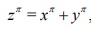; then x; y; and z are each divisible by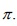 

Femat[2010]Primary 11Yxx

The special case Z⁴=X⁴+Y⁴ is impossible [1].In view of the fact,it is only neccessary to prove ,if x,y,z are relativaly prime postive integer, is odd prime ,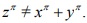(In this article ,the symbol  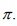will represt an odd prime