Prime ideals and Godel ideals of BL-algebras
DOI:
https://doi.org/10.24297/jam.v9i9.2237Keywords:
BL-algebra, Godel algebra, ideal, prime ideal, irreducible ideal, Godel ideal.Abstract
In this paper we give further properties of ideals of a BL-algebra. The concepts of prime ideals, irreducible ideals and Godel ideals are introduced. We prove that the concept of prime ideals coincides with one of irreducible ideals, and establish the Prime Ideal Theorem in BL-algebras. As applications of Prime ideal Theorem we give several representation and decomposition properties of ideals in BL-algebras. In particular, we give some equivalent conditions of Godel ideals and prove that a BL-algebra A satisfying condition (C) is a Godel algebra i the ideal f0g is a Godel ideal i all ideals of A are Godel ideals if and only if 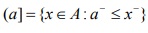 for any
for any 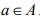
Downloads
Downloads
Published
How to Cite
Issue
Section
License
 All articles published in Journal of Advances in Linguistics are licensed under a Creative Commons Attribution 4.0 International License.
All articles published in Journal of Advances in Linguistics are licensed under a Creative Commons Attribution 4.0 International License.








