The Hermite Hadamard Inequality on Hypercuboid
DOI:
https://doi.org/10.24297/jam.v16i0.8053Keywords:
Convex function, Hermite--Hadamard's inequality, Jensen's inequalityAbstract
Given any a := (a1; a2,... ; an) and b := (b1; b2;... ; bn) in Rn. The n-fold convex function dened on [a; b], a; b 2 Rn with a < b is a convex function in each variable separately. In this work we prove an inequality of Hermite-Hadamard type for n-fold convex functions. Namely, we establish the inequality
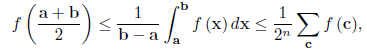
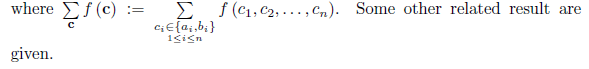
Downloads
Download data is not yet available.
Downloads
Published
2019-01-31
How to Cite
Alomari, M. W. (2019). The Hermite Hadamard Inequality on Hypercuboid. JOURNAL OF ADVANCES IN MATHEMATICS, 16, 8234–8246. https://doi.org/10.24297/jam.v16i0.8053
Issue
Section
Articles
License
 All articles published in Journal of Advances in Linguistics are licensed under a Creative Commons Attribution 4.0 International License.
All articles published in Journal of Advances in Linguistics are licensed under a Creative Commons Attribution 4.0 International License.








