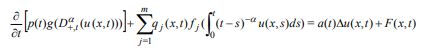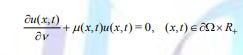FORCED OSCILLATION FOR A CLASS OF FRACTIONAL PARABOLIC PARTIAL DIFFERENTIAL EQUATIONS

Abstract

We investigate the oscillation of class of time fractional partial dierential equation
of the form

for (x; t) 2 R+ = G; R+ = [0;1); where
is a bounded domain in RN with a piecewise
smooth boundary @
; 2 (0; 1) is a constant, D +;t is the Riemann-Liouville fractional derivative
of order of u with respect to t and is the Laplacian operator in the Euclidean N- space RN
subject to the Neumann boundary condition

We will obtain sucient conditions for the oscillation of class of fractional partial dierential
equations by utilizing generalized Riccatti transformation technique and the integral averaging
method. We illustrate the main results through examples.